1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
| import struct
def read_data():
with open('memory.bin', 'rb') as f:
data = f.read()
# A: 1024
# B: 1040
# SBOX: 1056
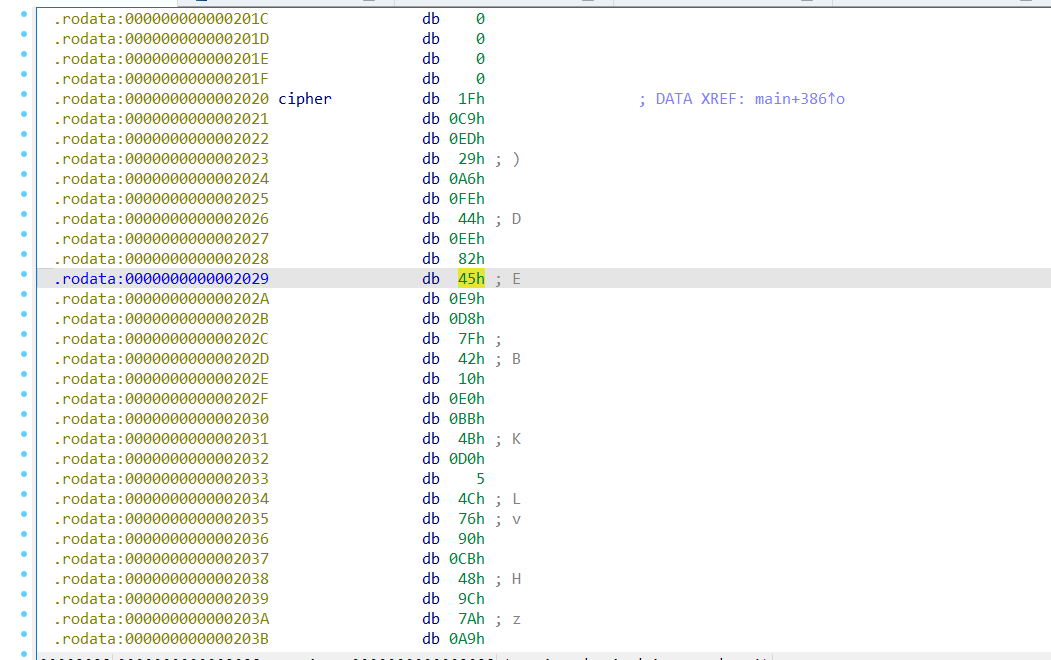
# CIPHERTEXT: 1312
A = list(data[1024:1040])
B = list(data[1040:1056])
SBOX = list(data[1056:1056+256])
CIPHERTEXT = list(data[1312:1312+32])
return A, B, SBOX, CIPHERTEXT
def generate_keys(A, B):
# Initial Key K0
K0 = [0] * 16
for i in range(16):
# Function 2: (A[i] ^ B[i]) - 23*i
val = (A[i] ^ B[i]) - (23 * i)
K0[i] = val & 0xff
Keys = [list(K0)]
# Round Keys K1..K10
# Logic: Kr[i] = Kr-1[i] ^ (r * 17) ^ i
for r in range(1, 11): # Rounds 1 to 10
prev_key = Keys[-1]
new_key = [0] * 16
for i in range(16):
val = prev_key[i] ^ (r * 17) ^ i
new_key[i] = val & 0xff
Keys.append(new_key)
return Keys
# Standard AES helpers
def inv_sub_bytes(state, inv_sbox):
return [inv_sbox[b] for b in state]
def inv_shift_rows(s):
# InvShiftRows is Shift Right 0, 1, 2, 3
# Row 0: 0, 4, 8, 12 -> No change
# Row 1: 1, 5, 9, 13 -> Shift Right 1 -> 5, 9, 13, 1
# Row 2: 2, 6, 10, 14 -> Shift Right 2 -> 10, 14, 2, 6
# Row 3: 3, 7, 11, 15 -> Shift Right 3 -> 15, 3, 7, 11
new_s = list(s)
# Row 1
new_s[1], new_s[5], new_s[9], new_s[13] = s[13], s[1], s[5], s[9]
# Row 2
new_s[2], new_s[6], new_s[10], new_s[14] = s[10], s[14], s[2], s[6]
# Row 3
new_s[3], new_s[7], new_s[11], new_s[15] = s[7], s[11], s[15], s[3]
return new_s
def xtime(a):
return (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)
def mul_bytes(a, b):
p = 0
for i in range(8):
if b & 1:
p ^= a
a = xtime(a)
b >>= 1
return p
def inv_mix_columns(s):
# Standard InvMixColumns
# 0e 0b 0d 09
# 09 0e 0b 0d
# 0d 09 0e 0b
# 0b 0d 09 0e
new_s = [0] * 16
for c in range(4):
offset = c * 4
# Note: input 's' is linear [0..15] where 0,1,2,3 is Col 0?
# Wait, ShiftRows treated 0,4,8,12 as Row 0.
# So memory layout is Column Major?
# WASM load8 offset=0,1,2,3 -> Col 0?
# Function 4 (MixColumns) loads 0, 1, 2, 3.
# It treats them as a column.
# So bytes 0,1,2,3 form a column.
# This means layout is Column 0: 0,1,2,3. Column 1: 4,5,6,7.
# ShiftRows code:
# Load 1 (Row 1 Col 0). Store 13 (Row 1 Col 3).
# This means 0,1,2,3 are NOT rows. They are a column.
# Row 0: 0, 4, 8, 12.
# Row 1: 1, 5, 9, 13.
# Row 2: 2, 6, 10, 14.
# Row 3: 3, 7, 11, 15.
# This is standard AES layout (Column-Major).
col = s[offset : offset+4]
new_s[offset] = mul_bytes(col[0], 0x0e) ^ mul_bytes(col[1], 0x0b) ^ mul_bytes(col[2], 0x0d) ^ mul_bytes(col[3], 0x09)
new_s[offset+1] = mul_bytes(col[0], 0x09) ^ mul_bytes(col[1], 0x0e) ^ mul_bytes(col[2], 0x0b) ^ mul_bytes(col[3], 0x0d)
new_s[offset+2] = mul_bytes(col[0], 0x0d) ^ mul_bytes(col[1], 0x09) ^ mul_bytes(col[2], 0x0e) ^ mul_bytes(col[3], 0x0b)
new_s[offset+3] = mul_bytes(col[0], 0x0b) ^ mul_bytes(col[1], 0x0d) ^ mul_bytes(col[2], 0x09) ^ mul_bytes(col[3], 0x0e)
return new_s
def add_round_key(state, key):
return [state[i] ^ key[i] for i in range(16)]
def decrypt_block(ciphertext_block, keys, inv_sbox):
state = list(ciphertext_block)
# Encryption structure:
# 1. AddRoundKey(K0)
# 2. Rounds 1..9: Sub, Shift, Mix, Add(Kr)
# 3. Round 10: Sub, Shift, Add(K10)
# Decryption: Reverse
# Inverse Round 10
state = add_round_key(state, keys[10])
state = inv_shift_rows(state)
state = inv_sub_bytes(state, inv_sbox)
# Inverse Rounds 9..1
for r in range(9, 0, -1):
state = add_round_key(state, keys[r])
state = inv_mix_columns(state)
state = inv_shift_rows(state)
state = inv_sub_bytes(state, inv_sbox)
# Inverse Initial AddRoundKey
state = add_round_key(state, keys[0])
print(f"Block input: {ciphertext_block}")
print(f"Block output: {state}")
return state
def solve():
A, B, SBOX, CIPHERTEXT = read_data()
# Generate Inverse SBox
INV_SBOX = [0] * 256
for i in range(256):
INV_SBOX[SBOX[i]] = i
print(f"A: {A}")
print(f"B: {B}")
print(f"SBOX sample: {SBOX[:16]}")
print(f"CIPHERTEXT: {CIPHERTEXT}")
Keys = generate_keys(A, B)
print(f"K0: {Keys[0]}")
print(f"K1: {Keys[1]}")
plaintext = []
# Process blocks
for i in range(0, len(CIPHERTEXT), 16):
block = CIPHERTEXT[i:i+16]
decrypted = decrypt_block(block, Keys, INV_SBOX)
plaintext.extend(decrypted)
print("Decrypted bytes:", plaintext)
try:
print("Decrypted string:", bytes(plaintext).decode('utf-8'))
# Unpad
pad_len = plaintext[-1]
if 0 < pad_len <= 16:
print("Unpadded:", bytes(plaintext[:-pad_len]).decode('utf-8'))
except:
print("Could not decode as utf-8")
if __name__ == '__main__':
solve()
# flag{One_Easy_Wasm_Chall}
|